录：
　　Part 1
　　Part 2
　　Part 3
　　Part 4

文档内容：
[Part 1]

在之前的 FSAA 簡介中，已經有稍微提到三角面的失真（aliasing）問題。不過，在該文章中，主要提到的方法，是在於消除三角面邊緣的 aliasing（通常是鋸齒現象）上面，而沒有提到貼圖方面的問題。而在這篇文章中，將會簡單介紹貼圖的失真問題，和目前 3D 加速晶片所使用的方法。

貼圖的失真問題，和一般繪製三角面的失真問題，有什麼不同的地方呢？最主要的差別，在於繪製貼圖是一個重新取樣（resampling）的過程。因為，貼圖本身也是一個數位影像。所以，貼圖已經是由一個訊號取樣後的結果。現在要把貼圖貼到三角面上，繪製三角面所需要的取樣點，並不一定會剛好是貼圖所使用的取樣點。所以，在這裡會出現二次取樣的情形。下圖是一個例子：

上圖中，左邊的白色格子是和螢幕上的像點對齊的，所以可以把它們看成是放大後的像點。右邊的格子，是相對於左邊這些放大後的像點。所以，可以看出來，當貼圖被貼在 3D 的三角面上時，它的取樣點會有很大的變化。而且，因為透視投影的原因，取樣的間距也不一定會是固定的。這會讓問題變得更複雜。

註：此圖是由 NVIDIA 所提供的 Show Footprint 程式產生的。

如果只看 1D 的訊號，那麼，重新取樣的過程，就是如下圖所示：

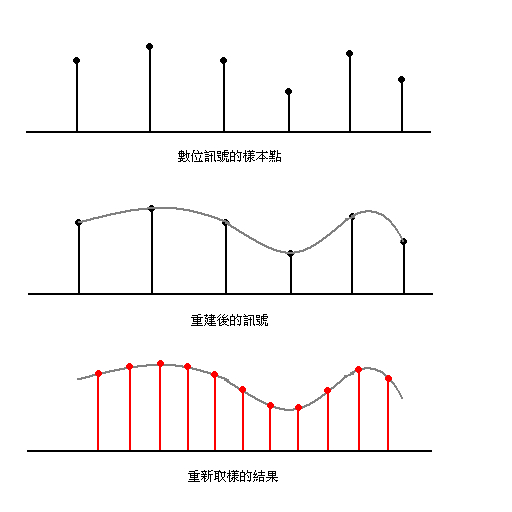
貼圖在被重新取樣的過程中，主要會面臨的問題有兩種：第一種就是放大的取樣，即取樣點的間距，比原先貼圖的取樣點間距要來得小；第二種是縮小的取樣，即取樣點的間距較大。上圖就是一個放大取樣的例子。


[Part 2]

重新取樣的第一個動作，就是要重建原來的訊號。如果重建訊號的動作不正確，就會在重新取樣的時候，造成失真的問題。按照訊號處理的理論，我們知道取樣後的訊號，只要其取樣頻率大於訊號頻率的兩倍（即 Nyquist frequency），就可以重建出原來的訊號。這在許多領域都常被使用，包括聲音處理的領域。在數位圖形的情形下又是如何呢？下面是一個例子：

原始訊號	重建訊號（使用 60x60 sinc filter）

可以看到重建出來的訊號有很嚴重的 ringing effect。這是二維訊號難以避免的結果。不過，用這種方法重建出來的訊號，倒是沒有什麼嚴重的 aliasing 問題。然而，利用這種方法重建訊號，是不太可能即時進行的，因為計算量實在是太大了。以上圖為例，上圖使用 60x60 的 sinc filter，所以對每個重新取樣的點，都需要做 60x60 個取樣點的計算。這樣的計算量是非常大的。

除了重建訊號的問題之外，如果重新取樣是縮小的取樣，也就是取樣點的間距變大的話，還需要一個額外的切除高頻成份的動作。這部分比較複雜，所以這裡先以放大的重新取樣為主。

為了要能夠快速重建出訊號，一定要使用簡單的運算。最簡單的運算，當然就是在重新取樣的時候，直接取距離最近的取樣點。因此，這個方法稱為 nearest sampling。因為只取一個取樣點，所以有時也稱為 point sampling。它的結果當然不會太好，而且還會產生新的失真問題。

其實 point sampling 也可以看成利用零次多項式（即常數多項式）去逼近的方法。所以，一個很自然的想法，就是用一次多項式去逼近，也就是線性內插（linear interpolation）。下圖是線性內插的示意圖：

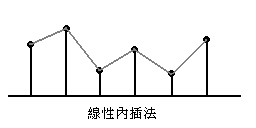
如果是在二維的訊號（像是 2D 貼圖）上，那就要同時對兩個方向都做線性內插，所以稱為雙線性內插（bilinear interpolation）。

使用雙線性內插的時候，每個取樣點需要取 2x2 個點來計算，所以計算量並不大。不過，線性內插的問題在於，它所產生的結果並非平滑的，所以在某些情形下，表現並不好。例如，下圖的例子中，字母 D 的右下角部分，以線性內插產生的結果，就還是有一些鋸齒狀的現象。

如果再提高逼近的次數，就是以三次多項式來逼近了，稱為 cubic interpolation。在二維的情形下，稱為 bicubic interpolation。三次內插有很多不同的型式，不過，對每個取樣點，它都需要 4x4 的計算。就目前的 3D 硬體來說，計算量已經是相當大，所以極少有 3D 硬體支援這種內插方式。不過，三次內插會產生平滑的訊號，所以一般來說，效果比線性內插要好一些。

下面是 point sampling、bilinear interpolation 和 bicubic interpolation 的例子。

Point sampling	Bilinear interpolation	Bicubic interpolation

一般來說，因為 bilinear interpolation 的效果已經相當不錯，再加上計算量又少，所以一般 3D 顯示晶片都是使用 bilinear interpolation 來處理貼圖的重新取樣問題，特別是在放大的部分。


[Part 3]

如果重新取樣時，取樣點的間距比原來要大，即縮小圖形的時候，就會出現新的問題。最明顯的問題，在於取樣點間距放大時，相對的，取樣頻率也就減少了。這時，訊號中就可能會包含一些過高的頻率成份。所以，這時候會需要一個 low pass filter。下面是一個極端的例子：

原始圖片	Point sampling	3×3 Gaussian filter	Adaptive filter

在上圖中，原始圖形具有相當多的高頻率成份，但是並沒有超出取樣頻率的一半，所以並沒有失真的現象。但是，如果直接進行重新取樣，縮小為原來的一半時，就會出現失真的現象。可以看出，在左上角以外的三個角落都出現了原先沒有的圓形。如果使用 3×3 的 Gaussian filter 再進行重新取樣，情形就會好一些，圓形變得較為不明顯。如果使用 adaptive box filter，失真的情形就幾乎看不到了。不過，一般情形下，它會有過度模糊的現象。

事實上，對一般的情形來說，簡單的 box filter 的效果就已經很好了。事實上，要找到一個「萬用」的 filter 恐怕是不可能的。如果一個 filter 能消除失真的情形，那它通常會過於模糊。反過來說，如果一個 filter 能產生較為清晰的結果，那它通常就沒辦法有效地消除失真。所以，要使用什麼 filter 往往和圖形本身有關。

不過，如果要即時運算的話，就不太可能利用這些 filter 了。因為，如果縮小的程度愈大，就會需要愈大的 filter 才行。例如，縮小 2 倍通常 2×2 的 box filter 就可以有良好的效果。但是，如果是縮小 4 倍，就會需要 4×4 的 box filter。對於即時運算的情形，這是很麻煩的問題。

為了解決這個問題，Lance William 在 1983 年的 ACM SIGGRAPH 提出了一篇重要的論文 "Pyramidal Parametrics"。這篇論文提出了一個解決方法：如果事先把貼圖用各種大小的 filter 處理，建立許多不同大小的貼圖。將來在縮小的時候，只要選擇適當的大小，就不需要使用超過 2x2 的 filter。這個方法就是 MIP map。MIP 為拉丁文 multum in parvo（即 many things in a small place）的縮寫。

舉個例子來說：如果貼圖的大小是 256×256，可以事先計算出 128×128、64×64、32×32、…、4×4、2×2 和 1×1 的貼圖。假設現在對貼圖做重新取樣，需要縮小 5 倍，這時只要取用 64×64 的版本就可以很快得到重新取樣的結果，而不需要再對原來的貼圖做 5×5 的 filter。當然，這樣會使貼圖所需的空間增加，但是最多只會增加原來的三分之一的空間。考慮到它在速度上的優勢，這點空間其實不算什麼。

不過，即使是使用 MIP map 也無法解決所有的問題。MIP map 必需配合適當的 filter 方式，才能在某些情形下，產生較佳的結果。


[Part 4]

現在我們來看一些 MIP map 的例子。假設現在路邊有三個一模一樣的路標，路標如下圖：

現在把這樣的路標，在近、中、遠三個距離各放一個。如果只使用一般的 bilinear filtering，結果如下圖：

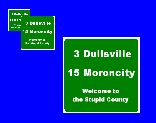
最前面的路標還算清楚，但是後面的兩個路標則變得亂七八糟。像是路標的白色邊緣，在後面的兩個路標就只顯示了一部分。如果使用了 MIP map 的話，結果就會好一些：

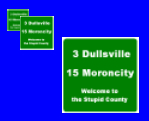
不過，如果對每個 pixel 只選擇某個 MIP map 的解析度，那可能會出現一些討厭的問題。在這裡用一條「路」做例子：

上圖中顯示出一條直路。它並沒有使用 MIP map，所以可以看到左邊的黃色斜線標誌在某個距離外，會出現一些環狀失真的現象。如果加上 MIP map，結果如下圖：

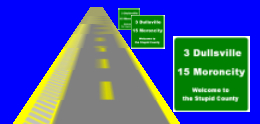
你可能會說：「哇！這是什麼鬼東西！」。很明顯的，它出現過度模糊的現象。不只如此，還可以看到令人討厭的接縫。這是因為在不同的距離，會需要不同解析度的貼圖。但是在轉換解析度的時候，並不能很平滑地轉換，所以才會出現接縫。

這個接縫的問題並不難解決，只要在兩個解析度的貼圖之間，也做線性的內插就可以了。這就是所謂的 trilinear filtering。它的結果如下圖：

可以看到，在使用 trilinear filtering 之後，雖然還是會有過度模糊的現象，但是至少接縫不見了。

為什麼會出現過度模糊的現象呢？這是因為這條路相對於觀察者來說，是相當「扁平」的。所以，它的一個 pixel 在貼圖上的 footprint 會變得很扁，比如說，可能是一個長寬比是 4:1 或更大的長方形。顯示晶片在決定要用哪個解析度的 MIP map 時，會選較低的解析度。所以，就會造成它在某個方向是適當的解析度，但是在另一個方向則會過度模糊。以上圖來說，在垂直方向的解析度是適當的，但是水平方向就不適當了。

一個簡單的方法，可以處理這個問題。我們可以強迫顯示晶片使用較高解析度的貼圖。比如說，如果我們知道 footprint 通常是在 4:1 左右的程度，那就可以強迫顯示晶片使用四倍解析度的貼圖。這稱為 MIP map 的 LOD bias。下面是兩個例子：

LOD bias = -1.0	LOD bias = -1.5

從上面的結果可知，設定 LOD bias 可以改善過度模糊的現象。但是，它同時也造成了失真。可以注意到左邊的黃色斜線標誌又出現一些環狀失真了。

所以 LOD bias 並不能解決所有的問題，而且它也只適用在一些特定的情形。不過，還有一個方法可以處理這種情形。如果我們已經知道某個貼圖的 footprint 總是很扁，而且知道它通常都會「扁」到某個程度（例如，4:1），那其實可以一開始就做一個很扁的貼圖。這對一些像是賽車遊戲的跑道特別有效。下面這個例子就是把路面的貼圖拉長為 4:1 後的結果：

它的效果很好。不過，這個方法只能用在方向是固定的情形，如果視角常常會轉動，那它可能反而會變得更為模糊。當然，對於一般視角變化不大的情形，像是一般的賽車遊戲，它是很不錯的做法。不過，對於像是第一人稱射擊、飛行模擬等視角變化較大的遊戲來說，這個方法就不見得這麼有用了。下圖是一個例子：

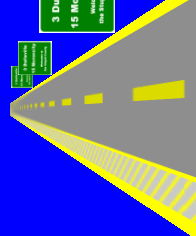
它在遠方的模糊情形仍相當不錯，並沒有明顯的過度模糊現象。但是在較近的地方，特別是黃色斜線標誌，就顯得過度模糊了。所以它並不是一個萬用的方法。

理想上的做法，是使用更多的 texel 來做 filtering。例如，如果 footprint 是一個 2:1 的長方形，那就取八個 texels 來做 filtering。如下圖：

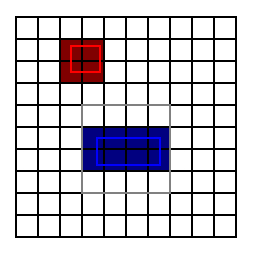
上圖中，亮紅色和亮藍色方框，分別是兩個 pixel 對貼圖的 footprint。亮紅色方框的長寬比並不大，只涵蓋了四個 texels，所以用一般的 bilinear filtering 就夠了。但是亮藍色方框就不一樣了，它的長寬比約略是 2:1，並涵蓋了八個 texels。所以，用一般的 bilinear filtering，會選擇解析度較低的貼圖。因此，它大略會把接近灰色方框的範圍內的 texels 做平均，所以會產生過度模糊的現象。

要避免過度模糊的現象，最簡單的方法，就是直接取它所涵蓋的八個 texels 來做平均。當然，這樣需要的計算量就比一般的 bilinear filtering 要大了。因為通常是在長寬比大於 1 的時候，才會需要這樣的做法，所以又稱為 anisotropic filtering。

當然，一般來說，顯示晶片的硬體並不能無限制去取得 texels。例如，某個硬體可能只支援存取八個 texels（若使用 trilinear 則是 16 個）。而且，因為長寬比愈大，就可能會需要取得愈多的 texels 來進行平均，這樣也可能會讓效能受到很大的影響。所以，一般來說，我們會指定一個最大的長寬比。也就是說，顯示晶片只需要處理長寬比到某個程度，例如 2:1。若長寬比超過這個數字，就只好讓它變得過度模糊了。這個數字通常稱為 maximum level of anisotropy。

下圖是把最大的長寬比設為 2 的情形：

因為它只處理長寬比到 2:1 的情形，所以在遠方過度模糊的情形，和把 LOD bias 設為 -1 是完全一樣的。不過，和 LOD bias 不同的是，它並沒有在黃色斜線標誌上，產生環狀失真的情形。

下圖是把最大的長寬比設為 16 的情形：

可以看到幾乎所有的失真，包括過度模糊的現象，都已經消失了。這樣的確是可以產生非常高品質的貼圖效果。不過，它的缺點也是很明顯的：對每個貼圖來說，使用 trilinear filtering 的情形下，最多會需要讀取 128 個 texels。這會需要很多顯示記憶體的頻寬，因此會造成效能降低。而且，也不是所有的顯示晶片都支援到這麼高的 anisotropic filtering。例如，NVIDIA 的 GeForce 256 和 GeForce 2 系列顯示晶片，就只支援到長寬比為 2 的 anisotropic filtering。